Numpy: ベクトルおよび行列計算を数値的計算によりサポート

Matplotlib: 関数グラフなどの表示

Sympy: 数式計算のライブラリ

VPython: 3D画像や動画を作成できる。

VScodeのデバックコンソールで出力が表示されない問題

https://hachian.com/2020/01/22/print_no_longer_provides_output_in_debug_console/

ライブラリのインストールコマンド

VSCodeのターミナルにて

(Pythonのpyファイルのフォルダーを指定して)

pip install Numpy　や　pip install Pandas　や　pip install Matplotlib

など。

from numpy import linspace, pi, sin, cos, exp
# numpy で定義されているlinspace, pi, sin, cos, expをimport
import matplotlib.pyplot as plt
#Matplotlibに含まれるライブラリpyplotをimport.
#as pltで pyplotで定義される名前は全てplt.の接頭語で参照できる。

x = linspace(-pi, pi, 101)
#linspaceとは、線形に配置された(間隔にある)ベクトルのこと。
#xは、-piからpiまでを100等分。両端を含む101個の点の等差数列
#-pi = x0, x1, ..., x100 = pi
#を表す。ここで,xo = x[0]で定義される。
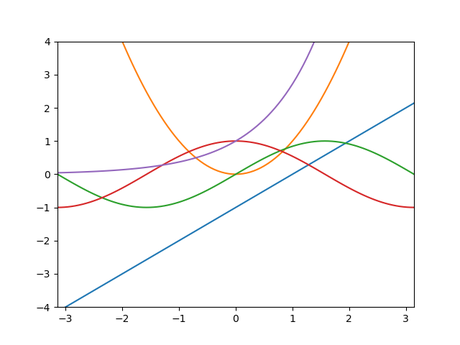
for y in [x -1, x**2, sin(x), cos(x), exp(x)]:
    plt.plot(x, y)
#y  = x-1, y =x^2, y = sin(x), y = cos(x), y = exp(x)のグラフを作成
#plt.plot(x, y)は, (xo, y0) ..., (x100, y100)の点を結んだ折れ線グラフ
plt.xlim(-pi, pi), plt.ylim(-4, 4), plt.show()
#グラフのx軸、y軸の描画する範囲を指定し、ディスプレイに描画。

import sympy
#sympyで定義される名前は全てsympy.　の接頭語で参照できるようになる。
#下記では、Sympyで定義されたsolveという名前であれば、sympy.solveとしてつかえる。
from sympy.abc import x, y
#.abs モジュールを使って、方程式の未知数に用いるシンボルx, yをインポート。

ans1 = sympy.solve([x + 2 * y - 1, 4 * x + 5 * y -2])
print(ans1)
#連立方程式を解く。方程式は=0の形に変形した左辺を並べて[と]で囲む。つまり、
# x + 2 * y - 1　= 0
# 4 * x + 5 * y -2 = 0
#を解いていることになる。
ans2 = sympy.solve([x**2 + x + 1])
print(ans2)
#二次方程式を解く。つまり
# x^2 + x + 1 = 0
#を解いていることになる。
ans3 = sympy.solve([x**2 + y**2 - 1, x - y])
print(ans3)
#連立二次方程式を解く。x^2 + y^2 = 1とy=xの交点を求めることになる。つまり、
# x**2 + y**2 - 1 = 0
# x - y = 0

{x: -1/3, y: 2/3}
[{x: -1/2 - sqrt(3)*I/2}, {x: -1/2 + sqrt(3)*I/2}]
[{x: -sqrt(2)/2, y: -sqrt(2)/2}, {x: sqrt(2)/2, y: sqrt(2)/2}]

import PIL.Image as Img
#PILのモジュールImageを Imgとしてimport

im0 = Img.open('Figure_1.png')
#画像ファイルをim0として見込み。パスを指定しない場合は、pyプログラムと同じところにいれておく。
print(im0.size, im0.mode)
#im0画像の大きさとカラー情報を表示
im1 = im0.convert('L')
#画像im0をグレースケールに変換して、im1を生成
im1.thumbnail((200, 200))
#im1の大きさを変更。縦横比は変更無し
print(im1.size, im1.mode)
#im1画像の大きさとカラー情報を表示
im1.save('Figure_1.jpg')
#画像を保存。

(640, 480) RGBA
(200, 150) L

def f(N):
#f(N)を定義。fを関数名、Nを仮因数。
    P = []
#Pの初期値を空に定義
    for n in range(2, N):
#変数nが2以上N未満の整数値を繰り返す。nはループカウンタ
        q = 1
#qを1としておいて、0になったらnは素数でないこととする。
        for p in P:
#ループカウンタpが素数のリストPの要素を動きながら、次の行からブロック最後の行まで繰り返す。
            q = n % p
#nをpで割って余りを計算する式。qは余り
            if q == 0:
                break
#条件節において、もしqが0であるならば(== 等符号、つまり余りがゼロ。つまり割り切れた和のこと)、breakによってfor pからのブロックを抜ける
        if q:
            P.append(n)
#qは0以外（つまり、qのブール値がtrue)ならば、整数nを新たな素数としてリストPに付け加える。
#ここまでが最初のfor文
    return P
#完成した素数リストPを返す。関数定義の後は、２行あけることが推奨されている。

if __name__ == '__main__':
#Pythonにおける慣用句。メインプログラムとして使用するときに記載する。
    P = f(20)
#Pの呼び出し。returnで返された戻り値Pを代入する。
    print(P)

[2, 3, 5, 7, 11, 13, 17, 19]